Face detection
Haar features
Haar filters are a tiny bit like predefined kernels. They are made up of black and white rectangles. An operation with these windows follows that we sum the pixels in the white regions and subtract the value from the sum of pixel values in the black region. For face detection, we primarily use 3 kinds of these filters - 2, 3 and 4 rectangle ones.
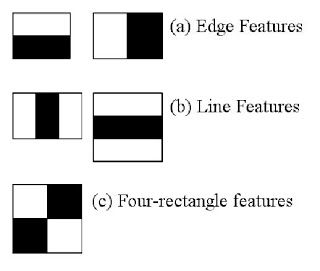
We would have to use these filters at different scales on each given image for all pixels (from the top right to the bottom left, sort of like how we do a convolution). To make these calculations more efficient, we make use of integral images.
Integral image
As an analogy, if an image can be thought of as a 2D discrete probability mass function, then its integral image would its 2D cumulative distribution function. Basically in the integral image, the value of each pixel is the sum of all pixels to the left and top of it.
If we calculate the integral image, we can find the sum of pixels in any arbitrary rectangular region in the image, using just 4 pixel values from its integral image. And obviously, this makes calculating Haar features significantly faster.
Computation
An integral image can be calculated in a single pass, if we row by row (like a raster scan). For every pixel's integral intensity, we add the top, left, top-left (diagonally) adjacent pixel values.
Feature maps
On operating with all the Haar features for a given scale, we get a vector (many) of feature maps (images showcasing feature response). And now we use this vector to train and classify input data. (Like say a nearest neighbour classifer. But the original paper mentions AdaBoost)